浅谈用统计分析方法助客户服务质量管理提升

客户世界 | 2023年1月12日 | 客世原创, 文库 | 评论已关闭 | 992

摘要：本文运用统计学中的时间序列模型和逻辑回归模型理论分析方法，通过分析客服中心历史业务记录数据，试探讨客户服务运营管理中通话接通率和客户满意度两个关键指标的提升，为运营管理者在数据分析工作中提供了统计学分析的思路和方法。

引言

伴随着市场竞争的越来越激烈,各个企业越来重视客户的体验,通过不断提升服务质量来改善客户体验，提高客户忠诚度，持续为企业创造更多的价值。对于整个企业来说，客服中心承担着与客户建立和维护好客户关系，因此质量管控一直是客服中心运营管理中的一个重点。现在大部分客服中心基本上采用座席软件系统，通过软件系统可以记录大量通话数据信息。这些信息可转化成不同的KPI管理指标。随着客服中心向精细化、数据化管理转型，运营者越来越重视这些KPI关键指标。通过数据驱动客服质量提升。

数理统计分析，是通过对历史数据的观察分析，运用数理统计相关理论方法建立模型,推断所研究的对象。通过应用统计学方法,可以找到因变量（研究对象）与其他变量之间的相关性,还能对因变量未来情况进行预测推断。本篇试应用经典的统计理论方法，来讨论客服中心运营管理中通话接通率和客户满意度两个关键服务质量管理指标的研究。也就是统计学理论中研究的因变量问题。

1.通话接通率管理指标

1.1 统计分析方法选择

目前在大部分客服中心影响通话接通率的主要因素是通话业务量和座席排班数量。对通话业务量的预测应该是座席安排的前提，为了实现人力资源的最优配置，不同的通话业务量应该配置不同数量的客服代表人员。因此为保持通话接通率在一定水平下，准确预测通话业务量是面临的一个很重要问题。

在统计学理论中，时间序列分析方法是目前发展成熟的一种动态数据序列分析算法，时间序列方法分析的主要研究目的之一就是根据历史记录的各时间段业务量数据，进行深入挖掘，发现一定规律，建模预测的方法。本文用某客服中心的业务数据来介绍用ARIMA时间序列模型进行预测的具体过程。

1.2 历史通话业务量分析

在正式应用建模前，我们通过折线图来对每日各时段的历史业务量记录进行观察，如图1。从图中可见，把业务量数据每日分成24个时段，业务量数据在不同时段有明显的周期性，因此用历史数据来预测未来数据具有现实意义。

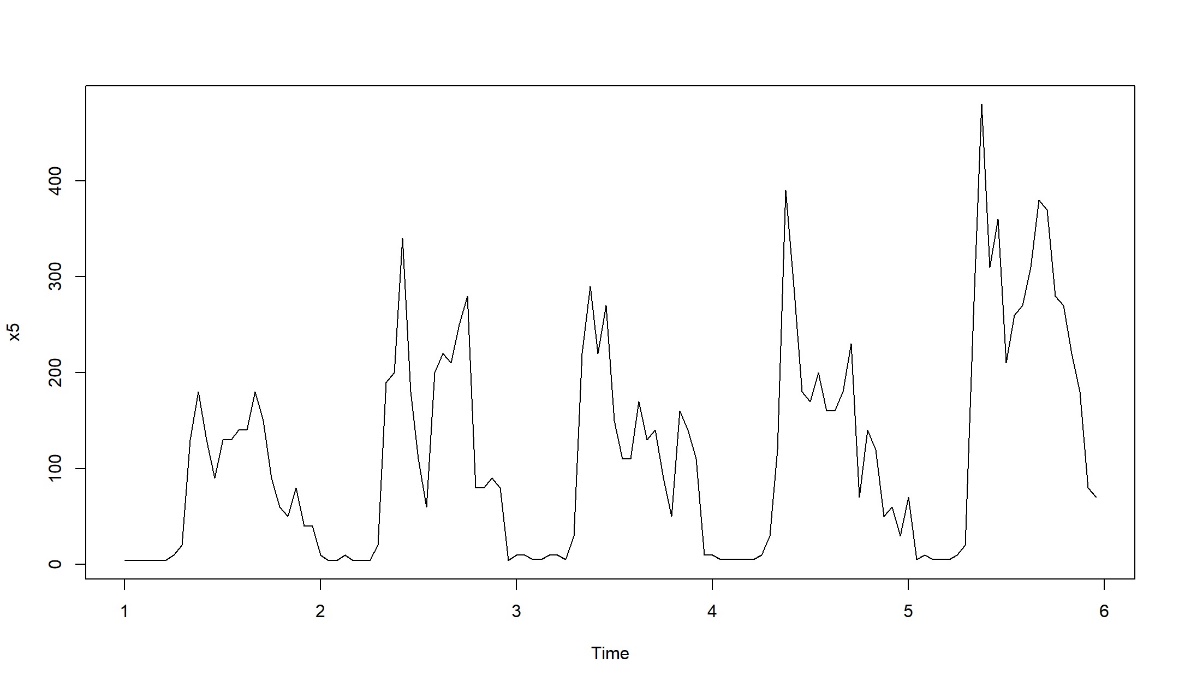
图1：每日各时段历史业务量记录

1.3 ARIMA模型的具体方法

在建模前，需要对历史业务数据进行整理加工预处理，提炼出具有时间序列的时序数据。在实际应用中，客服中心业务量每月、每周、每日、各时段等不同类型时间序列遵循不同变化规律，所以在分析预测时，需要根据实际业务需求选择从不同时间维度找变化规律进行建模分析。本篇用每日不同时段时间序列具体分析（如图1所示序列）。

ARIMA(p,d,q)模型是指d阶差分后自相关最高阶数为p，移动平均最高阶数为q的模型，通常包含p+q个独立的未知系数：

建立ARIMA模型的具体流程如图2所示：

图2：ARIMA建模流程

平稳性是ARIMA模型中的一个重要假设，针对蕴含一定线性趋势的序列进行d阶差分运算实现趋势平稳，通过使用自回归的方式提取确定性信息。观察我们本次分析的时序数据(图1)，发现还存在稳定的周期性（每日24时段一个周期），所以要考虑用季节乘积模型，构造原理简单地说，短期相关性用ARMA(p,q)模型提取，季节周期性用以周期步长S为单位的ARMA（P,Q）模型提取。假设短期相关和季节周期效应之间具有乘积关系，模型结构如下：

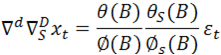
通过解线性方程组的特征根方式求得自相关系数和偏自相关系数，使用自相关ACF图和偏自相关PACF图来为ARIMA模型选定备选参数（即选定可能的p值和q值）。

图3给出了本次序列ACF和PACF图。

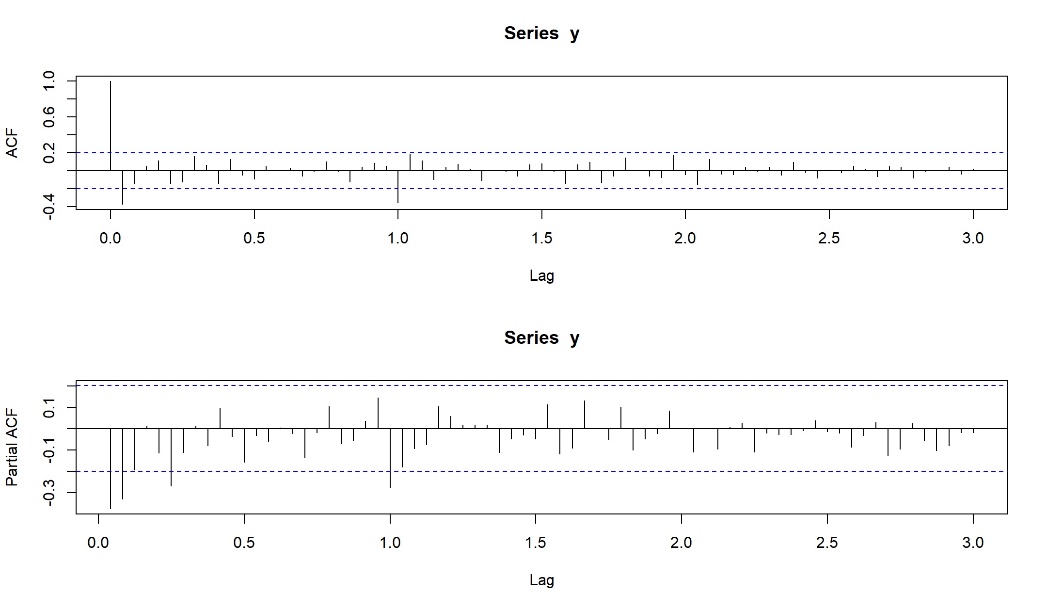
图3：本次序列ACF和PACF图

根据本次时序数据特征，因考虑到了周期效应(也称季节效应)、趋势效应和随机波动之间有着复杂相互关联性，简单的季节模型不能充分提取其中的相关关系，因此我们初步选定拟合季节乘积模型：ARIMA(0,1,1)(1,1,0)[24]。

判定是否是一个好的拟合模型，需要进行模型的显著性检验。一般来说，一个模型合适，那模型的残差序列应该为白噪声序列。反之，如果残差序列为非白噪声序列，那就意味着残差序列中还残留着相关信息未被提取，说明拟合模型不够有效。当一个模型通过了检验，说明在一定的置信水平下，该模型能有效地拟合观察值序列的波动，还需要进行选择相对最优的参数组合，检验每个系数是否都显著非零，使用AIC或BIC准则来评判模型的相对优劣。

我们本次拟合模型的具体参数如图4。

图4：软件运行结果截图1

当我们选定模型后，就可以用它来做预测了。图5画出了拟合预测效果图，实现了对未来24个时段的预测。从图中可以看出预测值与真实值的变化趋势基本一致，预测值与实际值之间的差别较小。因此估计模型具有较高的预测精度。

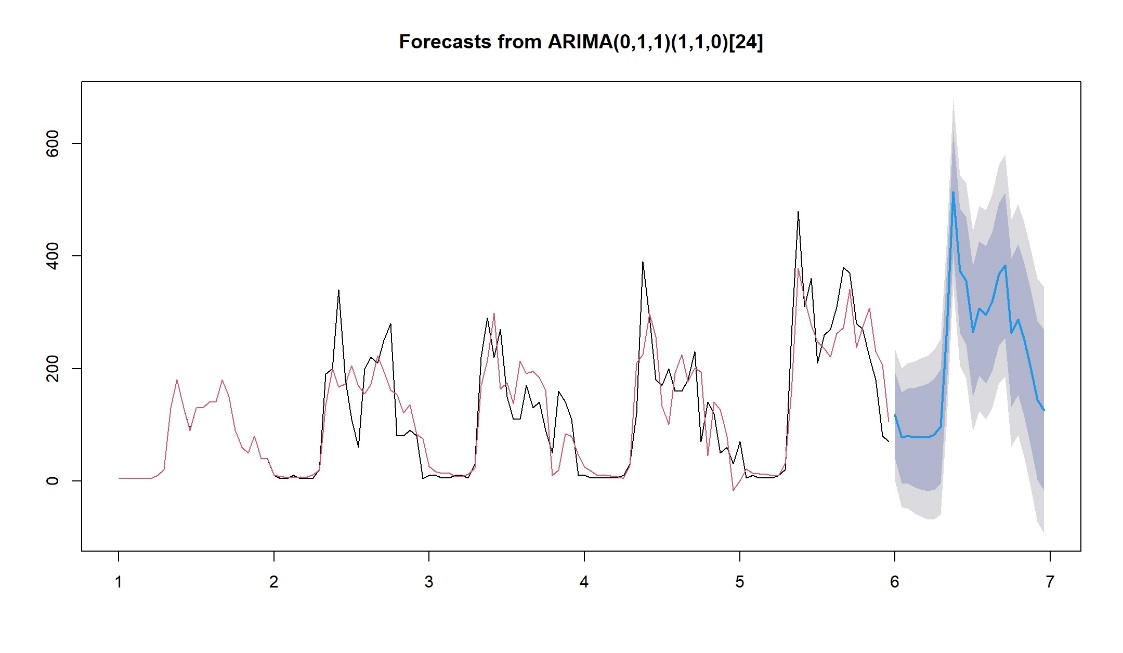
图5：拟合预测图

1.4小结

利用上述ARIMA预测模型，预测值表示为由最近的真实值和最近的预测误差组成的线性函数。因此，只要外推时间不长，使用线性随机模型进行预测能够保证一定的预测精度。所以运用时尽量根据动态变化的数据进行频度较高的预测。通过应用时序模型的预测方法比传统的凭经验预测提高了精度，能为排班提供快速、准确的预测话务量, 为更精确的排班创造了前提条件。通过匹配合适的客服代表数量，从而整体的客服通话接通率就有了保证。

2.客户满意度管理指标

2.1统计分析方法选择

现在客服中心多采用通话结束后语音满意度调查方式评定客户感受是否满意，具有一定客观性。本篇试想从每个通话记录的各种信息中深入挖掘一下，讨论客户评定满意是否与某些接线数据指标存在着显著相关关系，并依据此洞察规律并结合人工抽取质检的方式进一步分析验证原因，最终推动客户满意度提升。秉着这个思路，在统计方法中回归分析方法是通过建立统计模型研究变量间相互关系的密切程度、结构状态及进行模型预测的一种有效工具。

2.2变量选择确定及设计

回归分析是处理变量x与y之间关系的一种统计方法，如果变量x1,x2,…,xp与随机变量y之间存在着相关关系，通常每当 x1,x2,…,xp取值确定后，y便有相应的概率分布与之对应。模型表示如下：

其中y称为被解释变量（因变量）； x1,x2,…,xp称为解释变量（自变量）；为随机误差，引入后使得变量之间的关系描述为一个随机方程。在本次讨论的数据来自某客服中心通话业务数据，我们关心的问题是：满意度调查客户的评价是否满意，这就是研究的因变量。确定了因变量后，我们再考虑解释变量，在通话记录中一般能记录的通话特征包括通话类型、归属地、排队耗时、响铃时间、通话时长、通话时间、通话频率等，实际工作中可以考虑很多标签成为解释变量。本篇主要考虑通话时长、排队耗时和响铃时间三个变量

因我们涉及的因变量数据类型是定性数据，并且只有两个可能结果（满意或不满意），这样的因变量可以用虚拟变量（取值1或0）来表示。针对0-1型因变量可采用Logistic回归模型。对三个时间数据类型解释变量进行转化设计，其中通话时长转化成三个水平的定性数据（短时长、中时长、长时长）（具体见表1）。

表1：数据变量说明表

2.3逻辑回归分析具体思想

针对因变量y只能取值1或0两个离散值，不适合直接作为回归模型中的因变量，需要先变换成取值在[0,1]概率函数，再进行逻辑变换，对应的模型的数学形式如下:

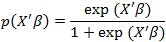
其中x’β=β0+β1×1+…βjxj 是回归系数β 和 x（解释变量）的线性组合。

逻辑回归分析中关心的是回归系数β ，解读是这样：如果βj >0,那么在给定其他解释变量不变的前提下，指标xj 的上升会带来条件概率p( x’β)的上升。也就是说，因变量取值为1的可能性会变大。反之如果 βj<0, 在给定其他解释变量不变的前提下，指标xj 的上升会带来条件概率p( x’β) 的下降。也就是说，因变量取值为0的可能性会变大。通过最大似然估计方法求解极大值来估算未知参数βj ，软件工具都会直接给出求解结果。

本次分析的数据模型结果如表2所示。解读如下：根据设定的以通话分类M（中时长）为基准组，在5%的显著性水平下，截距项高度显著，符号为正，这说明通话分类为“M”的影响客户评定满意（因变量取值为1可能性变大）。而哑变量THFL L和THFL S也是高度显著，符号为负，说明通话分类为“L”和“S”的影响客户评定不满意（因变量取值为0可能性变大），并且THFL S变量比THFL L变量的回归系数更小，说明通话分类“S”更加影响客户评定不满意。排队耗时（PDHS）和响铃时间（XLSJ）变量并不显著，但符号为负，也说明影响因变量取值为0可能性大。

表2：模型结果

因模型中还包含不显著的因素，因此接下来还可以考虑根据AIC准则和BIC准则，选择更加简洁的模型。本篇不在赘述这个环节。

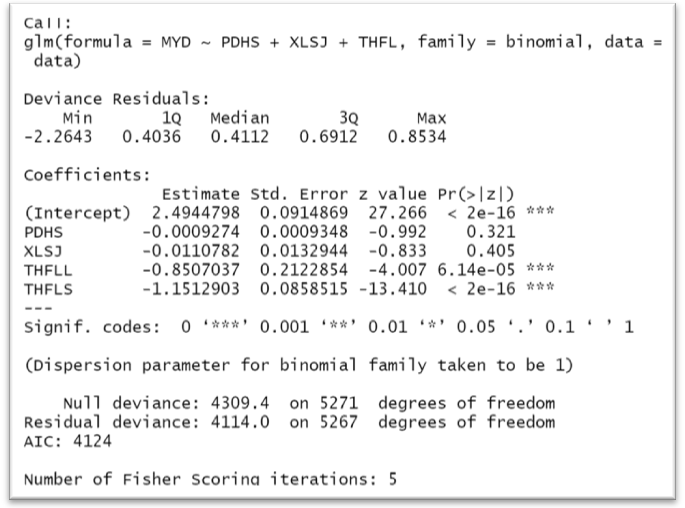
软件运行结果截图2

根据以上的分析结果，通话时长显著影响着客户评定满意。通过我们后期的人工录音质检进一步分析验证，发现在通话分类为“S”和“L”并用户评定不满意的的录音中大多都存在基础业务流程不熟、理解能力欠佳等问题，而在分析通话分类为“M”的录音中，体现出人员的引导能力较强，按照业务流程处理规范，体现很好的专业性。我们认为通话时长数据指标能从一个侧面体现了业务流程能力的高低，也就直接影响到了客户满意与否的感受。

2.4小结

通过以上逻辑回归分析方法得到的结果，为客服运营管理者在设计业务问题流程、优化话术上提供了一个很好的数据指导，即业务流程和话术安排控制在多长时间的通话是最优的效果，尤其是在偏技术类需要为客户提供远程技术支持的客服中心尤为重要。

我们用回归的统计方式单纯分析通话记录的数据信息，但客户真实感受是受多方面共同影响，客服代表的工作态度、实际业务处理能力技巧等都是重要的影响因素并没有在模型中考虑，这是在本次分析中存在的局限性。但不妨碍运用此统计分析方法思路，进行更加深入研究。比如可将通话信息再按照客户来电咨询的内容分成不同类型，可得到更加精准的不同业务流程最佳通话时长数据支持。

3.结语

本文通过对某客服中心历史业务数据的分析，利用时间序列理论和回归分析理论对客户服务运营管理中的关键指标进行了研究。现代统计软件工具和计算机运算能力的强大，统计模型中复杂的计算工作在计算机后台完成，在使用模型输出结果时非常的快捷。用统计学方法进行客户服务质量管理的数据分析最重要的是，从运营工作中的相关业务理解出发，深入如何把一个抽象的问题具体化和数据化，再设计合适的模型，最后运用模型来进行相关因素、决策预测、变量控制方面的分析，最终来提升客户服务质量管理工作。

参考文献：

[1] 王燕．应用时间序列分析［M］．中国人民大学出版社，2008．

[2] 李洁明，祁新娥．统计学原理［M］．复旦大学出版社，2017．

[3] 何晓群．应用回归分析［M］．电子工业出版社，2017．

[4] 王汉生，成慧敏．商务数据分析与应用-基于R［M］．中国人民大学出版社，2020．

[5] 牟颖，王俊峰，谢传柳，等．大型呼叫中心话务量预测[J]．计算机工程与设计，2010．

[6] 艾勇．电力呼叫中心话务量的指数平滑预测方法［J］．中南民族大学学报: 自然科学版，2012．

[7] 刘童．话务量时间序列预测方法的实现［D］．长春: 吉林大学，2008．

作者：孙廷超，来自中国人民大学。

本文刊载于《客户世界》2022年12月刊。